First, I’ll give you a little background. In the past I have discussed my use of curriculum created by the online math education community known as the MathTwitterBlogoSphere (MTBoS). I have already written about the use of and modifications for Fawn Nguyen‘s Visual Patterns and Christopher Danielson‘s Which Shape Doesn’t Belong.
So, I decided that what I can add to the community is to share how our classes are using the material from the MTBoS and how we are modifying it for students with disabilities. This is the first post in the series I am calling #MTBoS Mod(ification). The first subject of the series is the wonderful curriculum development website called Mathalicious. If you haven’t seen or used the work of this website, please take a minute to go to the link and poke around, but then come back here to see what modifications we made!
So here goes…
#MTBoS MOD: Mathalicious Edition
One of my classes has been working with the coordinate plane to introduce graphing skills and to provide a context for integers. The goals of the unit are pulled from the Common Core State Standards Initiative:
The beginning of the unit is referenced here. We used a Transition to Algebra task as a pre-assessment and a game called Humans vs. Zombies to introduce the properties of the coordinate plane (axes and ordered pairs).
Then in an effort to use these skills in a “real life” context we used the Mathalicious lesson called Icy Hot. Please read the lesson plan as written by Mathalicious before reading on…
I determined there were three skills we needed to review before engaging in the Mathalicious lesson as written. These were: range, scale, and thinking about the coordinate plane as a line graph.
To introduce the context I began with the part of the Mathalicious lesson that includes the five day forecast for your location.
This is a fantastic way to engage any population of students, because they are inherently interested in the weather (especially if snow days are in the forecast!) This was also the perfect opportunity to introduce the term range. Each student was asked to find the temperature range for each day and then the range for the whole week. If you’ve read ahead in the Mathalicious lesson, then you know that this is in preparation for what the students are asked to do further on in the lesson.
Next, we moved to a quick investigation of using different scales for the axes of a coordinate plane. I posted a closeup of the blank coordinate plane in Q1 of the Icy Hot lesson with the title of the graph covered. I asked the students what they noticed and what they wondered about the coordinate plane they were looking at. Answers varied, but all came back to the differing scales of numbers on the x-axis and the y-axis. The x-axis is counting by 1s and the y-axis is counting by fives. My favorite answer was that the x-axis was counting by fourths, which is technically true. Though since it was not the focus of the lesson, I acknowledged the student’s awesome observation, but quickly moved on to the scaled whole numbers.
Once I unveiled the fact that this coordinate plane actually was a graph of the high and low temperature vs. month, I asked what they thought the x and y-axes represented. This was a quick conversation, because there is no 20th month. Sometimes in special education math classes quick conversations are a good thing.
Once we had reviewed range and scale we were ready to graph!
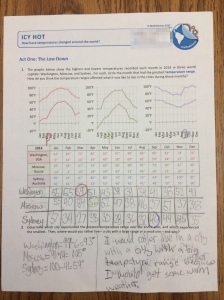
I asked the students to just graph the Washington DC portion of Q1 on a large piece of graph paper (two 8×11 pieces taped together!) This allowed the students a hands-on method of reviewing the highs and lows of Washington DC’s temperatures for the year. Then we asked them to find the month with the largest range.
Some students calculated the ranges under the graph (pictured above) and some used a table (pictured below).
Once they had finished their graph of Washington DC and made their choice of largest ranges we gave them the Mathalicious handout which also shows the data for Moscow and Sydney. This was an opportunity for the students to use some estimation in order to look at the new (smaller, thus more challenging) graphs and make an estimated guess as to which month had the largest range. The natural curiosity and competitiveness took over as each student “needed” to find out if they were right by calculating ALL of the ranges for Moscow and Sydney, which for students who struggle with maintaining focus and sustained engagement was a success unto itself. For the rest of the lesson we followed the Mathalicious handout for Act 1.
We only completed Act 1 of the Mathalicious lesson, but it still ends with a fantastic application of the work in question #2 on the worksheet, “Would you rather live in a city with a small or large range of temperatures?” The Mathalicious lesson was easy to follow for students and teachers. The lesson has both hardcopy and interactive versions of the information. The interactive graphs were also super fun to play with especially for the students!
Special thanks to Mathalicious for a wonderful lesson and being the first focus of this series!















Pingback: #MTBoS Mod: Estimation 180 Edition | The Learning Kaleidoscope
Pingback: #MTBoS Mod: 3-Act Edition | The Learning Kaleidoscope
Awesome! Two questions:
1. What prompted you to create graphs on graph paper? Were the graphs in the handout too small, or did you think they gave away too much information by bring pre-filled (or both)?
2. How did students respond to the question about where they’d rather live: in a location with a higher or lower temperature range?
Great stuff. Thanks for sharing!
LikeLike
Hi Karim, thanks for the questions!
1. The main reason we created the graphs by hand was to assess the student’s abilities to create coordinate planes using appropriate tools and models (i.e. rulers and perpendicular number lines). The ones on the handout were a little too small for some students, but after creating one big graph by hand most students were able use the other two handout graphs to answer the questions competently.
2. Since range was a new concept for my class, I think they responded very well to the final question. We reviewed the term, its meaning, and usage in several contexts throughout the lesson in preparation for that final question. Then when it came time to answer it, the students required much less prompting or support than they may have needed without the embedded contextual practice.
I hope that answers your questions!
LikeLike